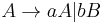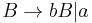Uniquely inversible grammar
A uniquely inversible grammar is a formal grammar where no two distinct productions give the same result. This implies the specific production can be inferred from its results.
Formal definition
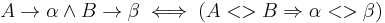
Examples
- Uniquely inversibles
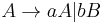
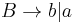
- Not uniquely inversibles